DIY random generation of binary and general trees


(ns my.m$macros)
(require '[reagent.core :as r])
(require '[reagent.ratom :as ratom])

DIY random generation of binary and general trees

Berlin - Feb 24, 2018


;; A live-coding presentation made with klipse
;; (thank you Yeonathan/viebel!)
(defn showme [s] [:h3 (str s)])
[:div (showme (js/Date.))]

Who am I? frederic.peschanski@lip6.fr — fredokun @ github

associate professor at Sorbonne University (ex-UPMC)
researcher at the Lip6 computer science laboratory
(live) programming & maths geek
long-time Lisper (scheme, CL, clojure(script))

Agenda

Generating binary trees
Genearting general trees

Remark: this presentation is a complement to the main presentation
about Boltzmann sampling.

Warning ! this presentation is code heavy! The whole source code is in the slides,
we’ll need to skip some parts (but you can play with the whole bunch online…)

Random sources (from test.check)

(require '[clojure.test.check.random
         :refer [make-random  ;; create source with seed
	         split        ;; two generators from one
		 rand-double  ;; uniform double in range [0.0;1.0[
		 rand-long    ;; uniform long (64 bits java, js ?)
		 ]])

;; generate a double between 0.0 (inclusive) and 1.0 (exclusive)
(defn next-double [src]
  (let [[src' src''] (split src)] ;; XXX: throw src?
    [(rand-double src') src'']))

(next-double (make-random 424242))

""

;; generate an integer in some range
(defn next-int [src mini maxi]
  (let [[x src'] (next-double src)]
    [(int (+ (* (- maxi mini) x)
             mini)) src']))

(next-int (make-random 424242) 24 450)
""

;; coin flips
(defn next-bool [src]
  (let [[x src'] (next-double src)]
    [(< x 0.5) src']))  ;; XXX: random bits leak !

(next-bool (make-random 424242))
""

Binary trees

(require '[clojure.spec :as s])

;; a spec for binary trees (with keyword labels)
(s/def ::bintree
  (s/or :tip nil?
        :node (s/tuple ::label ::bintree ::bintree)))
(s/def ::label int?)

;; example
(def ex-btree [1,
               [2 nil nil],
               [3 [4 nil,
                   [5 nil nil]],
               [6 nil nil]]])

(s/valid? ::bintree ex-btree)
""

Random generation from spec (via test.check):

(require '[clojure.test.check.generators :as gen])

(gen/generate (s/gen ::bintree) 10)
""

Observations
- non-uniform generation (it’s biased but don’t know how)
- lack of control: biased towards (very) small trees

Generating binary trees with test.check

Let's try the dedicated support for recursive structures

(def node-gen (fn [inner-gen]
                (gen/tuple gen/int inner-gen inner-gen)))

(def bt-gen (gen/recursive-gen node-gen (gen/return nil)))

(gen/generate bt-gen 10)
""

Observations
- non-uniform generation (it’s biased but don’t know how)
- lack of control: small-ish trees

Uniformity?

Unbiased sampling means sampling in the uniform distribution.

Defined for a combinatorial class:

each object has a finite size n
there is a finite number Cn of objects of a given size
uniform distribution: the probability of sampling an object of size n
is (/ 1.0 Cn)

Binary trees as a combinatorial class:

the size n of a tree is its number of (internal) nodes
but what about Cn?
⇒ Catalan numbers

Catalan numbers: counting binary trees

;; a point = a node or a tip (a `nil`)
(defn nb-points [n] (+ (* 2 n) 1))

;; a tip = a `nil` value
(defn nb-tips [n] (inc n))

;; counting binary trees (https://oeis.org/A000108)
(defn catalans
  ([] (cons 1 (cons 1 (catalans 1 1))))
  ([n Cn] (lazy-seq (let [Cn+1 (* (/ (* 2 (nb-points n))
                                     (nb-tips (inc n)))
	        		Cn)]
		    (cons Cn+1 (catalans (inc n) Cn+1))))))

(take 10 (catalans))
""

nil ;; tree of size 0

A beautiful bijection

<academic-stuff>

</academic-stuff>

The generation algorithm

Incremental generation of a binary tree uniformly at random
(a.k.a. Remy algorithm)

Input: a tree of size n taken uniformly at random
i.e. obtained with probabilty (/ 1.0 (nth (catalans) n))

Example: [1 [2 nil nil] [3 nil nil]]

Step 1: we pickup a "point" (either a node or a nil) uniformly at random
⇒ we need a random integer between 0 and (* 2 n)
Example: we pickup the 4th point: [1 [2 nil <nil>] [3 nil nil]]

Step 2: We select a direction, either left or right
⇒ We need a random boolean (coin flip)
Example: :left

Step 3: We build the tree of size n+1 according to the bijection, and remove the "mark"
Example: [1 [2 nil [4 <nil> nil]] [3 nil nil]]

Finally, the generated tree is: [1 [2 nil [4 nil nil]] [3 nil nil]]

⇒ this tree has been taken with probability (/ 1.0 (nth (catalans) (inc n)))
(proof is easy thanks to the bijection… but let’s skip it)

Tree representation

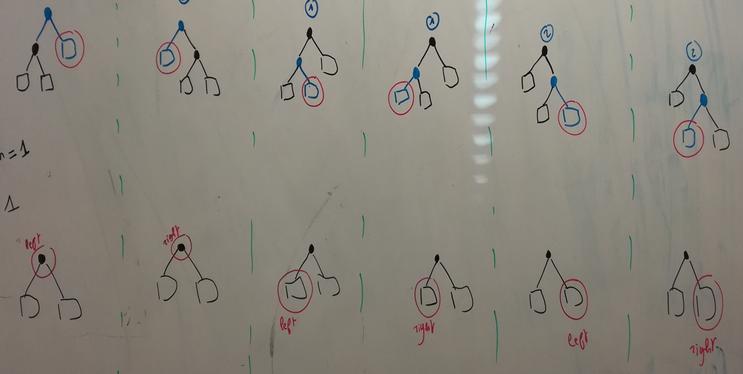
Step 1 (pickup a "point") is O(n) if we use the "classical" representation of binary trees.

⇒ Alternative "vectorized" representation to achieve "almost" O(1)

(defn root [lbl]
  [[lbl nil 1 2] #{0} #{0}])

(defn append-leaf [vtree lbl parent side]
  (let [[_ _ pleft pright] (nth vtree parent)
        pside (if (= side :left) pleft pright)
        tip-idx (count vtree)]
    [(-> vtree
       (assoc pside [lbl parent tip-idx (inc tip-idx)])
       (conj #{pside} #{pside})) pside]))

;; representation of [:a nil nil]
(root :a)
""

;; [:a [:b nil nil] nil]
(-> (root :a)
    (append-leaf :b 0 :left))
""

;; [:a [:b nil [:c nil nil]] nil]
(-> (root :a)
    (append-leaf :b 0 :left) (first)
    (append-leaf :c 1 :right))
""

From classical to vectorized binary trees

;; remark: tail-recursive
(defn vbuild
  ([t]
   (if-let [[lbl left right] t]
     (vbuild (root lbl) 0 :left left (list [0 :right right]))
     []))
  ([vtree parent side t cont]
   ;; a node
   (if-let [[lbl left right] t]
     (let [[vtree' nparent] (append-leaf vtree lbl parent side)]
       (recur vtree' nparent :left left (cons [nparent :right right] cont)))
     ;; a nil
     (if-let [[[parent' side' t'] & cont'] cont]
       (recur vtree parent' side' t' cont')
       vtree))))

(vbuild [:a [:b nil nil] nil])
""

Interlude: folding vectorized trees

;; the root is the only node with a  `nil` parent
(defn search-root [vtree]
  (loop [vtree vtree, idx 0]
    (if (seq vtree)
      (if (and (vector? (first vtree))
               (nil? (second (first vtree))))
        idx
        (recur (rest vtree) (inc idx)))
      ;; not found
      nil)))

;; a tail-recursive folder for vtrees
;; (let's skip the details...)
(defn vfold
  ([f init vtree]
   (let [root-idx (search-root vtree)]
     (vfold f init root-idx vtree '())))
  ([f init node-idx vtree cont]
   (cond
     (int? node-idx)
     (let [node (nth vtree node-idx)]
       (if (vector? node)
         (let [[lbl _ left-idx right-idx] node]
           (recur f init left-idx vtree (cons [::right lbl init right-idx] cont)))
         ;; tip
         (recur f init nil vtree cont)))
     ;; continuation (tail-recursion)
     (seq cont)
     (case (ffirst cont)
       ::right (let [[_ lbl racc right-idx] (first cont)]
                 (recur f racc right-idx vtree (cons [::finish lbl init] (rest cont))))
       ::finish (let [[_ lbl lacc] (first cont)]
                  (recur f (f lbl lacc init) nil vtree (rest cont))))
     :else ;; no more continuation
     init)))

(vfold #(+ 1 %2 %3) 0 (vbuild [:a nil [:b [:c nil [:d nil nil]] [:e nil nil]]]))
""

From vectorized to classical binary trees

;; typical fold one-liner
(defn vunbuild [vtree]
  (vfold vector nil vtree))

(vbuild [:a [:b nil nil] [:c nil nil]])
""

Apply the bijection = "Grafting"

Code size alert: grafting has several subcases
(let’s skip the details…)

(defn reparent [vtree parent old-child new-child]
  (update vtree parent (fn [[plbl pparent pleft pright]]
                         (if (= pleft old-child)
                           [plbl pparent new-child pright]
                           [plbl pparent pleft new-child]))))

(defn newchild [lbl parent side other new]
  (case side
    :left [lbl parent other new]
    :right [lbl parent new other]))

(defn graft [vtree lbl where side]
  (let [wnode (get vtree where)
        graft-idx (count vtree)]
    (if (vector? wnode)
      ;; <<either a node>>
      (let [[wlbl wparent wleft wright] wnode]
        ;; node case
        (as-> vtree $
            (if wparent (reparent $ wparent where graft-idx) $)
            (assoc $ where [wlbl graft-idx wleft wright])
            (conj $ (newchild lbl wparent side where (inc graft-idx))
                  #{graft-idx})))
      ;; <<or else a tip>>
      (let [parent (first wnode)]
        (-> vtree
            (reparent parent where graft-idx)
            (assoc where #{graft-idx})
            (conj (newchild lbl parent side where (inc graft-idx))
                  #{graft-idx}))))))
""

Grafting examples

(vunbuild (root :a))
""

(root :a)
""

(vunbuild (-> (root :a)
              (graft :b 0 :left)))
""

The random generation algorithm

(defn rand-bintree [src nb size vtree]
  (if (= nb size)
    [vtree src]
    (let [;; step 1: pickup a "point"
          [pos src'] (next-int src 0 (dec (count vtree)))
	  ;; step 2: choose side: left (true) or right (false)
          [left src''] (next-bool src')]
      (recur src'' (inc nb) size
             ;; step 3: apply bijection
             (graft vtree (keyword (str (inc nb))) pos (if left :left :right))))))

(rand-bintree (make-random 424242) 1 20 (root :1))
""

Observations
- uniform generation (we’ll see)
- controllable: the size parameter … is … the size of the tree
- efficient: generate quite large trees (linear time algo, tail-recursive)

Uniformity?

The theory (analytic combinatorics) gives an asymptotic for the average height of binary trees.

(defn avg-height-theory [size]
  (* 2.0 (Math/sqrt (* Math/PI size))))

(avg-height-theory 1000)
""

Let’s check this …

(defn vheight [vtree]
  (vfold #(+ 1 (max %2 %3)) 0 vtree))

(defn rand-bintrees [src size]
  (lazy-seq (let [[vtree src'] (rand-bintree src 1 size (root :1))]
               (cons vtree (rand-bintrees src' size)))))


(defn avg-height-practice [seed nb size]
  (/ (reduce + 0 (map vheight (take nb (rand-bintrees (make-random seed) size))))
     nb))

;; (time (avg-height-practice 14922 50 1000))
""

General trees

(s/def ::gentree (s/tuple keyword? (s/coll-of ::gentree :kind vector?)))

(def ex-rtree [:1 [[:2 [[:3 []]
                        [:4 [[:5 [[:6 []]]]]]]]
                   [:7 []]
                   [:8 [[:9 []]
                        [:10 []]
                        [:11 []]
                        [:12 []]]]]])

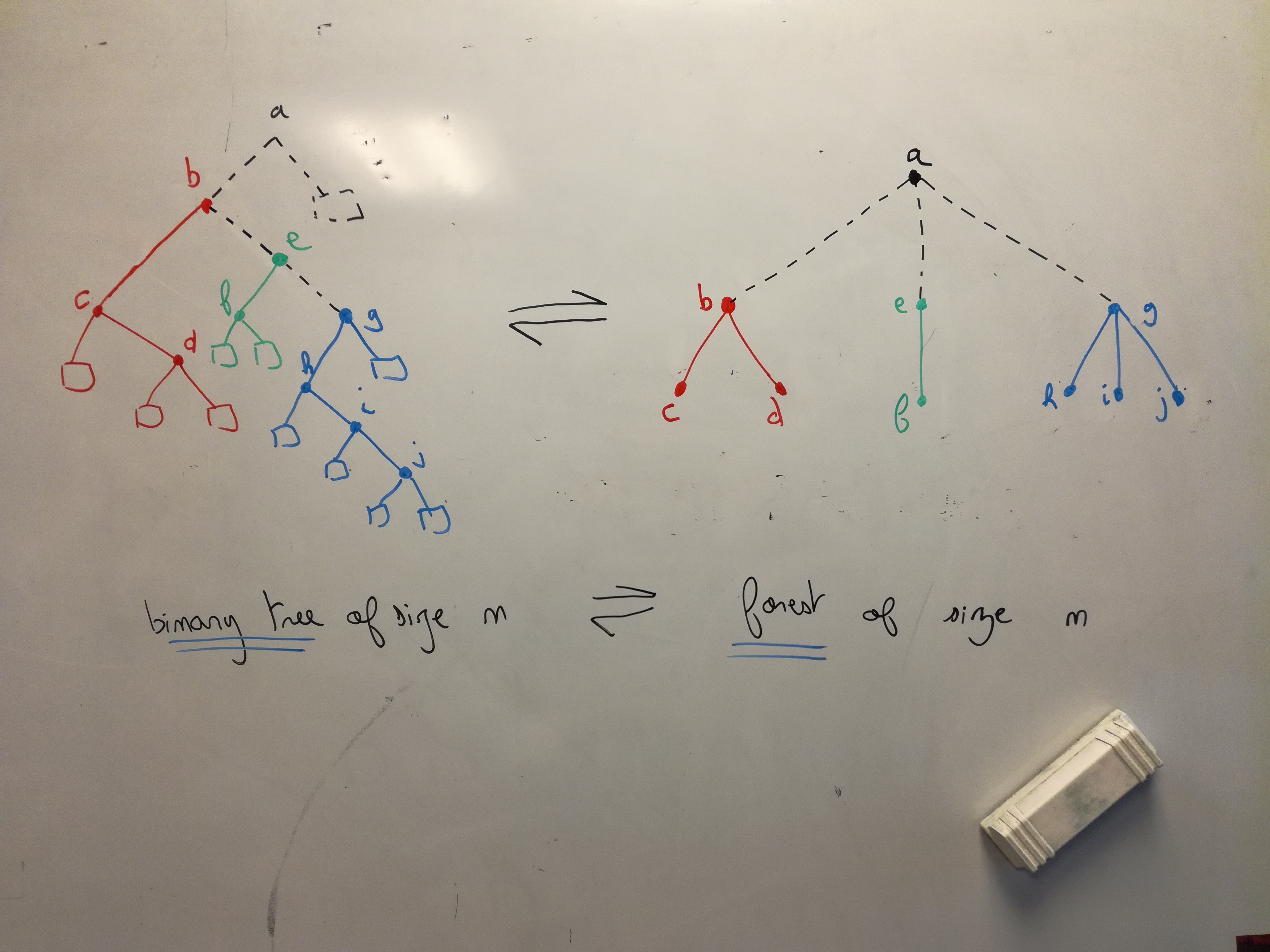
(s/valid? ::gentree ex-rtree)

Uniform random generation of general trees?

From binary to general trees (and vice-versa)

Yet another bijection.

<academic-stuff>

</academic-stuff>

Random generation of general trees

Step 1 : generate a binary tree uniformly at random (size n)

(def mybtree (-> (rand-bintree (make-random 424242) 1 10 (root :1))
                 (first)
		 (vunbuild)))

mybtree
""

Step 2 : convert it to a forest (size n)

(defn btree->forest [bt]
  (if (nil? bt)
    '()
    (let [[lbl left right] bt
          lefts (btree->forest left)
          rights (btree->forest right)]
      (cons [lbl (into [] lefts)]
            rights))))

(btree->forest mybtree)
""

Step 3 : add a root to obtain a general tree (size n+1)

(def mygtree [:0 (into [] (btree->forest mybtree))])

mygtree
""

Observation
- the forest is generated uniformly for size n
- the general tree is generated uniformly for size n+1
(there is only one way to put the root node)

The uniform random generator for general trees

(defn rand-gentree [src size]
  (let [;; step 1 : generate a binary tree uniformly at random
         [vtree src'] (rand-bintree src 1 size (root :1))
          btree (vunbuild vtree)
          ;; step 2 : convert to a forest
         forest (btree->forest btree)
          ;; step 3 : add a root
         gtree [:0 (into [] forest)]]
   [gtree src']))

(first (rand-gentree (make-random 424242) 20))
""

=> that's all folks!

← →